BLOQUE I
utilizas ángulos, triángulos y relaciones métricas.
ÁNGULOS
De acuerdo a las definiciones científicas, los ángulos son aquellas figuras constituidas por la conjunción de dos líneas en un punto común o vértice. Para que un ángulo se forme, las líneas que forman parte del proceso no pueden ser paralelas entre sí ya que eso implica que no hay contacto entre ambas y por tanto no se forma ninguna superficie común entre ellas.
Como es bien
conocido, hay diferentes tipos de ángulos y el grado de inclinación o el tamaño del mismo
dependerán de la distancia que separe a las dos o más líneas intervinientes
en la figura.
Clasificación
Angulo recto = 90º 
Angulo obtuso = mas de 90º 
Angulo convexo = a menos de 180º 
Angulo llano = 180º 
Angulo nulo = 0º 
Según su posición:
Los ángulos consecutivos poseen el mismo vértice y un lado en común
Los ángulos adyacentes, en cambio, conforman un ángulo llano ya que tienen un vértice y un lado en común y los otros lados ubicados uno en prolongación de otro.
Los ángulos opuestos por el vértice son los que comparten el mismo vértice y los lados de uno son la prolongación de los lados del otro.
Clases de ángulos según su suma:
Hay
dos clases de ángulos los complementarios que devienen de la
sumatoria de dos ángulos cuyo resultado es de 90°:
Los ángulos suplementarios, en cambio, son el resultado de dos ángulos cuya sumatoria dé como resultado 180°
Ángulos entre paralelas y una recta transversal
En los ángulos correspondientes, como muestra la figura, b y f son iguales:
En los ángulos alternos internos, en cambio, α y β son iguales:
En los ángulos alternos externos 1 y 4 son iguales, como lo muestra la figura:
Con respecto a una circunferencia, los ángulos que existen son los siguientes:
A)Ángulo central: es aquel que posee en el centro de la circunferencia su vértice y sus lados son dos radios.
B)Ángulo inscrito: es aquel cuyo vértice está en la circunferencia y sus lados son secantes a ella.
c) Ángulo semiinscrito: está en la circunferencia. En este ángulos uno de sus lados es secante y el otro tangente a la misma.
D)Ángulo exterior: es aquel que tiene su vértice en el exterior de la circunferencia.
e) Ángulo interior: es aquel que tiene su vértice en el interior de la circunferencia.
TRIÁNGULOS
Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados, es decir: no colineales). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo.Por lo tanto, un triángulo tiene 3 ángulos interiores, 3 ángulos exteriores, 3 lados y 3 vértices.Si está contenido en una superficie plana se denomina triángulo, o trígono, un nombre menos común para este tipo de polígonos. Si está contenido en una superficie esférica se denomina triángulo esférico. Representado, en cartografía, sobre la superficie terrestre, se llama triángulo geodésico.
Por las longitudes de sus lados
Triángulo equilátero: es un triángulo con tres lados iguales y tres ángulos congruentes.
Triángulo isósceles: es un triangulo con dos lados iguales y uno desigual.
triángulo escaleno: es un triangulo con todos sus lados desiguales.

Por la amplitud de sus lados
- Triángulo rectángulo: si tiene un ángulo interior recto (90°). A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.
- Triángulo oblicuángulo: cuando ninguno de sus ángulos interiores son rectos (90°). Por ello, los triángulos obtusángulos y acutángulos son oblicuángulos.
- Triángulo obtusángulo: si uno de sus ángulos interiores es obtuso (mayor de 90°); los otros dos son agudos (menores de 90°).
- Triángulo acutángulo: cuando sus tres ángulos interiores son menores de 90°. El triángulo equilátero es un caso particular de triángulo acutángulo.
 |  |  |
| Rectángulo | Obtusángulo | Acutángulo |
| Oblicuángulos | ||
Clasificación según los lados y los ángulos
Los triángulos acutángulos pueden ser:
- Triángulo acutángulo isósceles: con todos los ángulos agudos, siendo dos iguales, y el otro distinto. Este triángulo es simétrico respecto de su altura

- Triángulo acutángulo escaleno: con todos sus ángulos agudos y todos diferentes, no tiene eje de simetría.

- Triángulo acutángulo equilátero: sus tres lados y sus tres ángulos son iguales; las tres alturas son ejes de simetría (dividen al triángulo en dos triángulos iguales).
 Los triángulos rectángulos pueden ser:
Los triángulos rectángulos pueden ser:
- Triángulo rectángulo isósceles: con un ángulo recto y dos agudos iguales (de 45° cada uno), dos lados son iguales y el otro diferente: los lados iguales son los catetos y el diferente es la hipotenusa. Es simétrico respecto a la altura de la hipotenusa, que pasa por el ángulo recto.

- Triángulo rectángulo escaleno: tiene un ángulo recto, y todos sus lados y ángulos son diferentes.
 Los triángulos obtusángulos pueden ser:
Los triángulos obtusángulos pueden ser:

- Triángulo obtusángulo isósceles: tiene un ángulo obtuso, y dos lados iguales que son los que forman el ángulo obtuso; el otro lado es mayor que éstos dos.

- Triángulo obtusángulo escaleno: tiene un ángulo obtuso y todos sus lados son diferentes.
propiedades de los triángulos
1 Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.
a < b + c
a > b - c
2La suma de los ángulos interiores de un triángulo es igual a 180°.
A + B + C =180º
3 El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes.
α = A + Bα = 180º - C
5 Si un triángulo tiene dos lados iguales, sus ángulos opuestos también son iguales
ejercicios
1. De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Calcula los restantes elementos.
Resolución de un triangulo conociendo dos lados y el angulo comprendido
2. De un triángulo sabemos que: a = 10 m, b = 7 m y C = 30°. Calcula los restantes elementos.
Resolver un triángulo conociendo dos lados y un ángulo opuesto
sen B > 1. No hay solución
sen B = 1 Triángulo rectángulo
sen B < 1. Una o dos soluciones
3. Supongamos que tenemos a, b y A; al aplicar el teorema de los senos puede suceder:
1. sen B > 1. No hay solución.
Resolver un triángulo conociendo los tres lados
5. Resuelve el triángulo de datos: a = 15 m, b = 22 m y c = 17 m.
Cálculo de la altura de un punto de pie inaccesible
6. Se fija en el plano horizontal dos puntos A y C, y se mide la distancia que los separa: b= 500 m.
Se miden con el teodolito los ángulos A y C. A= 72º 18′ y C= 60º 32′.
También se mide el ángulo HAB = 62º 5′
Cálculo de la distancia entre dos puntos, uno de los cuales es inaccesible
7. Se fija en el plano horizontal dos puntos A y C, y se mide la distancia que los separa: b= 200 m.
Se miden con el teodolito los ángulos A y C. A= 61º 28′ y C= 54º 53′.
Cálculo de la distancia entre dos puntos inaccesibles
8. Se fija en el plano horizontal dos puntos C y D, y se mide la distancia que los separa: b= 450 m.
Se miden con el teodolito los ángulos C y D. C= 68º 11′ y D= 80º 40′.
También se miden los ángulos BCD = 32º 36′ y ADC = 43º 52′.
BLOQUE II
La congruencia de triángulos
criterios de congruencia
Los criterios de congruencia de triángulos nos dicen que no es necesario verificar la congruencia de los 6 pares de elementos ( 3 pares de lados y 3 pares de ángulos), bajo ciertas condiciones, podemos verificar la congruencia de tres pares de elementos.
Primer criterio de congruencia: LLLDos triángulos son congruentes si sus tres lados son respectivamente iguales.a ≡ a’b ≡ b’c ≡ c’→ triáng ABC ≡ triáng A’B'C’
b ≡ b’
c ≡ c’
α ≡ α’
→ triáng ABC ≡ triáng A’B'C’
b ≡ b’
α ≡ α’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’
a ≡ a’
b ≡ b’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’
Ejercicios de la congruencia de triangulos
1.Se tienen los angulos consecutivos \AOB;\BOC y \COD, siendo: \AOC = 47 ;\BOD = 51 ; y \AOD =
80 : Hallar la medida del \BOC:
Soluci on: Primero calculamos la medida de \COD. \COD = \AOD \AOC = 80 47 = 33 : Entonces
\BOC = \BOD \COD = 51 33 = 18 :
2. Hallar la medida de un angulo, sabiendo que su complemento y suplemento suman 208 :
Soluci on: Sea x la medida del angulo pedido. Entonces, seg un el enunciado (90 x) + (180 x) = 208 :
Entonces, 270 2x = 208 ) de donde 2x = 62 y de all x = 31 :
3. El doble del complemento de un angulo, m as el triple del suplemento del mismo, es 500 . Hallar la medida del
angulo.
Soluci on: Sea x la medida del angulo pedido. Entonces, seg un el enunciado 2(90 x) + 3(180 x) = 500 :
Entonces, 180 2x+540 3x = 500 ) de donde 720 5x = 500 y de all 5x = 220 concluyendo que x = 44 :
4. El suplemento del complemento de un angulo es igual a 3/2 de la diferencia entre el suplemento y el complemento
de dicho angulo.
Soluci on: Sea x la medida del angulo pedido. Entonces, seg un el enunciado:180 º - (90 º- x) =3/2(180º-x)-(90º-x)90º + x = 3/2(180º-x-90º+x)90º+x=3/2(90º)
90º+x= 135º
x= 45º
5. Dada la recta
!
PQ y un punto O sobre ella, a un mismo lado se trazan los rayos
!
OA y
!
OB, tal que
!
OA sea
interior al \POB y \AOP = 54 : Hallar la medida de \AOB si \QOB es el suplemento del triple de \BOA.
Soluci on: Seg un el enunciado:
\POA + \AOB + \BOQ = 180
Entonces 54 + x + (180 3x) = 180 de donde se obtiene que x = 27 :
6. Hallar la medida del \AFE si los segmentos AB y CD son paralelos y se sabe que \EFG = 100 y \DIH =
3\BFG.
Soluci on: Primero hallamos el valor de \BFG. Si trazamos una paralela a los segmentos AB y CD por el punto
G tendr amos que los angulos \FGI = \BFG + \GID dado los angulos alternos internos que se generan. Por
tanto, 100 = \BFG+180 3\BFG, de donde se obtiene que \BFG = 40 : Luego, \EFB = 100 \BFG
entonces \EFB = 60 y por ello \AFE = 120 º.
7.Sean los angulos consecutivos \AOB;\BOC; y \COD; siendo 2(\AOB) = 3(\COD); \AOB = 92 y\BOD = 76 . Hallar la medida del \BOC.
Soluci on: Por hip otesis, 2\AOB = 3\COD. Como
8.Las medidas de dos angulos suplementarios son entre s , como 3 a 7. Hallar el complemento del menor.
Soluci on: Sea x la medida del menor. El suplemente medir a entonces 180 x: Seg un el enunciado, x180x = 37 :Resolviendo, x = 54 por lo que el complemento es 90 54 = 36.
9.Si los 3/2 del complemento de un angulo es igual al suplemento del complemento del mismo angulo. Hallar .
Soluci on: Seg un enunciado planteamos la ecuaci on: 3
2 (90 ) = 180(90 ) de donde se tiene que 135 3
2 =90 + luego 135 90 = 32 + , por lo que 45 = 5 2 y por ello = 18:
5. Dada la recta
!
PQ y un punto O sobre ella, a un mismo lado se trazan los rayos
!
OA y
!
OB, tal que
!
OA sea
interior al \POB y \AOP = 54 : Hallar la medida de \AOB si \QOB es el suplemento del triple de \BOA.
Soluci on: Seg un el enunciado:
\POA + \AOB + \BOQ = 180
Entonces 54 + x + (180 3x) = 180 de donde se obtiene que x = 27 :
6. Hallar la medida del \AFE si los segmentos AB y CD son paralelos y se sabe que \EFG = 100 y \DIH =
3\BFG.
Soluci on: Primero hallamos el valor de \BFG. Si trazamos una paralela a los segmentos AB y CD por el punto
G tendr amos que los angulos \FGI = \BFG + \GID dado los angulos alternos internos que se generan. Por
tanto, 100 = \BFG+180 3\BFG, de donde se obtiene que \BFG = 40 : Luego, \EFB = 100 \BFG
entonces \EFB = 60 y por ello \AFE = 120 º.
10.La suma de las medidas de dos angulos es 80 y el complemento de la medida del primero es igual al doble dela medida del segundo. Calcular la diferencia de dichos angulos.
Soluci on: Sean x e y las medidas de los angulos en menci on. Por dato, x + y = 80: Tambi en se tiene que90x = 2y entonces x+2y = 90: Pero separando convenientemente x+y+y = 90 donde 80+y = 90 obteniendo que y = 10: Luego x = 70 y la diferencia pedida es 60.

BLOQUE III
Problemas de semejanza de triángulos y teorema de Pitagoras
criterios de semejanza
.


 2 Dos triángulos son semejantes si tienen los lados proporcionales.
2 Dos triángulos son semejantes si tienen los lados proporcionales.


 3 Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.
3 Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.



Razona si son semejantes los siguientes triángulos:





Son semejantes porque tienen los lados proporcionales.


180º − 100º − 60º = 20º
Son semejantes porque tienen dos ángulos iguales.



Son semejantes porque tienen dos lados proporcionales y un ángulo igual.
Teorema de Tales
Si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.
Ejercicios
1.Las rectas a, b y c son paralelas. Halla la longitud de x.

2.Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b? Sí, porque se cumple el teorema de Thales.
Sí, porque se cumple el teorema de Thales.

El teorema de Thales en un triánguloDado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los deltriángulo ABC.

Hallar las medidas de los segmentos a y b.


Aplicaciones del teorema de Thales
El teorema de Thales se utiliza para dividir un segmento en varias partes iguales.
Dividir el segmento AB en 3 partes iguales

1. Se dibuja una semirrecta de origen el extremo A del segmento.

2. Tomando como unidad cualquier medida, se señalan en la semirrecta 3 unidades de medida a partir de A.

3. Por cada una de las divisiones de la semirrecta se trazan rectas paralelas al segmento que une B con la última división sobre la semirrecta. Los puntos obtenidos en el segmento AB determinan las 3 partes iguales en que se divide.
Teorema de Pitagoras
El teorema de Pitágoras
En primer lugar deberíamos recordar un par de ideas:
- Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
- En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos.

Teorema de Pitágoras.- En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Demostración:

Si tenemos un triángulo rectángulo como el del dibujo del enunciado del teorema podemos construir un cuadrado que tenga de lado justo lo que mide el cateto b, más lo que mide el cateto c, es decir b+c, como en la figura de la derecha.
El área de este cuadrado será (b+c)2.

Si ahora trazamos las hipotenusas de los triángulos rectángulos que salen tendremos la figura de la izquierda. El área del cuadrado, que es la misma de antes, se puede poner ahora como la suma de las áreas de los cuatro triángulos rectángulos azules (base por altura partido por 2):

más el área del cuadrado amarillo . Es decir, el área del cuadrado grande también es el área del cuadrado pequeño más 4 veces el área del triángulo:
. Es decir, el área del cuadrado grande también es el área del cuadrado pequeño más 4 veces el área del triángulo:

Podemos igualar las dos formas de calcular el área del cuadrado grande y tenemos:

si ahora desarrollamos el binomio , nos queda:

que después de simplificar resulta lo que estábamos buscando:

problemas

1 La hipotenusa de un triángulo rectángulo mide 405.6 m y la proyección de un cateto sobre ella 60 m. Calcular:1 Los catetos.2 La altura relativa a la hipotenusa.3 El área del triángulo.
2 Calcular los lados de un triángulo rectángulo sabiendo que la proyección de uno de los catetos sobre la hipotenusa es 6 cm y la altura relativa de la misma  cm.
cm.
3 Una escalera de 10 m de longitud está apoyada sobre la pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura alcanza la escalera sobre la pared?
4 Determinar el lado de un triángulo equilátero cuyo perímetro es igual al de un cuadrado de 12 cm de lado. ¿Serán iguales sus áreas?
5Calcular el área de un triángulo equilátero inscrito en una circunferencia de radio 6 cm.
6Determinar el área del cuadrado inscrito en una circunferencia de longitud 18.84 cm.
7 En un cuadrado de 2 m de lado se inscribe un círculo y en este círculo un cuadrado y en este otro círculo. Hallar el área comprendida entre el último cuadrado y el último círculo.
8 El perímetro de un trapecio isósceles es de 110 m, las bases miden 40 y 30 m respectivamente. Calcular los lados no paralelos y el área
.9 A un hexágono regular 4 cm de lado se le inscribe una circunferencia y se le circunscribe otra. Hallar el área de la corona circular así formada.
10 En una circunferencia una cuerda mide 48 cm y dista 7 cm del centro. Calcular el área del círculo.
11 Los catetos de un triángulo inscrito en una circunferencia miden 22.2 cm y 29.6 cm respectivamente. Calcular la longitud de la circunferencia y el área del círculo.
12Sobre un círculo de 4 cm de radio se traza un ángulo central de 60°. Hallar el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente.
13 Un triángulo rectangulo tiene catetos 7 y 9
respectivamente, Calcular la hipotenusa.
c es la hipotenusa
c² = 7² + 9²
c² = 49 +81
c = √(130)
c=11.4018
14 Un triángulo rectángulo que también es
isosceles tiene una hipotenusa de 14 cm calcular la
medida de sus
catetos.
como es un
triángulo isosceles entonces tiene dos catetos iguales, por lo tanto:
a² + a² = 14²
2a² = 196
a² = 196/2
a= √(98)
a= 9.86
cada uno de los
catetos mide 9.86
15 Se
tiene un triángulo equilatero de 10 cm por lado calcular su área.
fórmula del
triangulo b.h/2
la base es 10
la altura es B² =
10² - (10/2)² ---------(B es un cateto)
C² = 100 -25
C= √(75)
C= 8.66
entonces la
fórmula del Área queda:
bXH/2
(10)(8.66)/ 2
43.3
el Área es 43.3 cm
16 Los
lados de un triángulo rectángulo estan dados por: x, x-2, x+2; Obtener la
medida de cada lado.
el teorema dice:
C² = A² + B²
entones
sustituimos:
C² = (x+2)²
A² = (x)²
B² = (x-2)²
(x)² + (x-2)² =
(x+2)²
desarrollamos los
binomios al cuadrado:
x² + x² -4x +4 =
x² + 4x +4
x² - 8x = 0
factorizamos y
buscamos sus 2 raíces:
x² - 8x = (x-8)(x)
x1 = 8 y x2 = 0
entonces las
medidas son:
X
= 8
x+2
= 10
x-2
= 6
17 Un triángulo rectángulo tiene un cateto de 8
cm y su hipotenusa mide 2cm mas que su otro cateto, Calcular la medida de cada
lado.
8² + x² = (2+x)²
64 + x² = 4 +4x +
x²
60 = 4x
x= 60/4
x= 15
un
cateto = 15cm
el
otro cateto conocido es de 8cm
y
la hipotenusa es de 17
BLOQUE IV
Reconoces la propiedades de los polígonos
Polígonos
Definición
Un polígono es la región del plano limitada por tres o más segmentos.Los polígonos son formas bidimensionales. Están hechos con
líneas rectas, y su forma es "cerrada" (todas las líneas están
conectadas).
Elementos de un polígono

Lados: Son los segmentos que lo limitan.
1 La hipotenusa de un triángulo rectángulo mide 405.6 m y la proyección de un cateto sobre ella 60 m. Calcular:1 Los catetos.2 La altura relativa a la hipotenusa.3 El área del triángulo.
2 Calcular los lados de un triángulo rectángulo sabiendo que la proyección de uno de los catetos sobre la hipotenusa es 6 cm y la altura relativa de la misma  cm.
cm.
3 Una escalera de 10 m de longitud está apoyada sobre la pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura alcanza la escalera sobre la pared?
4 Determinar el lado de un triángulo equilátero cuyo perímetro es igual al de un cuadrado de 12 cm de lado. ¿Serán iguales sus áreas?
5Calcular el área de un triángulo equilátero inscrito en una circunferencia de radio 6 cm.
6Determinar el área del cuadrado inscrito en una circunferencia de longitud 18.84 cm.
7 En un cuadrado de 2 m de lado se inscribe un círculo y en este círculo un cuadrado y en este otro círculo. Hallar el área comprendida entre el último cuadrado y el último círculo.
8 El perímetro de un trapecio isósceles es de 110 m, las bases miden 40 y 30 m respectivamente. Calcular los lados no paralelos y el área
.9 A un hexágono regular 4 cm de lado se le inscribe una circunferencia y se le circunscribe otra. Hallar el área de la corona circular así formada.
10 En una circunferencia una cuerda mide 48 cm y dista 7 cm del centro. Calcular el área del círculo.
11 Los catetos de un triángulo inscrito en una circunferencia miden 22.2 cm y 29.6 cm respectivamente. Calcular la longitud de la circunferencia y el área del círculo.
12Sobre un círculo de 4 cm de radio se traza un ángulo central de 60°. Hallar el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente.
13 Un triángulo rectangulo tiene catetos 7 y 9 respectivamente, Calcular la hipotenusa.
c es la hipotenusa
c² = 7² + 9²
c² = 49 +81
c = √(130)
c=11.4018
14 Un triángulo rectángulo que también es
isosceles tiene una hipotenusa de 14 cm calcular la
medida de sus
catetos.
como es un
triángulo isosceles entonces tiene dos catetos iguales, por lo tanto:
a² + a² = 14²
2a² = 196
a² = 196/2
a= √(98)
a= 9.86
cada uno de los
catetos mide 9.86
15 Se
tiene un triángulo equilatero de 10 cm por lado calcular su área.
fórmula del
triangulo b.h/2
la base es 10
la altura es B² =
10² - (10/2)² ---------(B es un cateto)
C² = 100 -25
C= √(75)
C= 8.66
entonces la
fórmula del Área queda:
bXH/2
(10)(8.66)/ 2
43.3
el Área es 43.3 cm
16 Los
lados de un triángulo rectángulo estan dados por: x, x-2, x+2; Obtener la
medida de cada lado.
el teorema dice:
C² = A² + B²
entones
sustituimos:
C² = (x+2)²
A² = (x)²
B² = (x-2)²
(x)² + (x-2)² =
(x+2)²
desarrollamos los
binomios al cuadrado:
x² + x² -4x +4 =
x² + 4x +4
x² - 8x = 0
factorizamos y
buscamos sus 2 raíces:
x² - 8x = (x-8)(x)
x1 = 8 y x2 = 0
entonces las
medidas son:
X
= 8
x+2
= 10
x-2
= 6
17 Un triángulo rectángulo tiene un cateto de 8
cm y su hipotenusa mide 2cm mas que su otro cateto, Calcular la medida de cada
lado.
8² + x² = (2+x)²
64 + x² = 4 +4x +
x²
60 = 4x
x= 60/4
x= 15
un
cateto = 15cm
el
otro cateto conocido es de 8cm
y
la hipotenusa es de 17
BLOQUE IV
Reconoces la propiedades de los polígonos
Polígonos
Definición
Un polígono es la región del plano limitada por tres o más segmentos.Los polígonos son formas bidimensionales. Están hechos con líneas rectas, y su forma es "cerrada" (todas las líneas están conectadas).
Lados: Son los segmentos que lo limitan.
Vértices: Son los puntos donde concurren dos lados.
Ángulos interiores de un polígono: Son los determinados por dos lados consecutivos.
Suma de ángulos interiores de un polígono: Si n es el número de lados de un polígono: Suma de ángulos de un polígono = (n − 2) · 180°
Diagonal: Son los segmentos que determinan dos vértices no consecutivos.
Numero de diagonales de un poligono: Si n es el número de lados de un polígono: Número de diagonales = n · (n − 3) : 2
4 · (4 − 3) : 2 = 2

5 · (5 − 3) : 2 =5 6 · (6 − 3) : 2 = 9
6 · (6 − 3) : 2 = 9
CIRCUNFERENCIA EXTERIOR: se llama circunscrita (aveces también incirculo) y conecta los vértices del polígono.CIRCUNFERENCIA INTERNA: se llama inscrita y toca cada lado del polígono en el punto medio.EL RADIO de la circunferencia circunscrita es tambien el radio del polígono.El radio de la circunferencia inscrita es el apotema del polígono.CLASIFICACIÓN DE POLÍGONOS:Los polígonos se clasifican en base a tres criterios:1) según el numero de lados2) según el numero de ángulos3) según la relación entre ángulos y lados
CLASIFICACIÓN DE POLÍGONOS SEGÚN LA CANTIDAD DE LADOS:
Triángulos
Tienen 3 lados.
Cuadriláteros
Tienen 4 lados.
Pentágonos
Tienen 5 lados.
Hexágonos
Tienen 6 lados.
Heptágonos
Tienen 7 lados.
Octágonos
Tienen 8 lados.
Eneágono
Tiene los 9 lados.
Decágono
Tiene 10 lados.
Endecágono
Tiene 11 lados.
Dodecágono
Tiene 12 lados.
Tridecágono
Tienen 13 lados.
Tetradecágono
Tiene 14 lados.
Pentadecágono
Tiene 15 lados.
Hexadecágono
Tiene 16 lados.
Heptadecágono
Tiene 17 lados.
Octadecágono
Tiene 18 lados.
Eneadecágono
Tienen 19 lados.
Icoságono
Tiene 20 lados.
Según sus ángulos
Convexos
Todos sus ángulos menores que 180°.
Todas sus diagonales son interiores.
Cóncavos
Si un ángulo mide más de 180°.
Si una de sus diagonales es exterior.
Angulo central

Ángulo central de un polígono regular
Es el formado por dos radios consecutivos.
Si n es el número de lados de un polígono:
Ángulo central = 360° : n
Ángulo central del pentágono regular= 360° : 5 = 72º
Ángulo interior de un polígono regular
Es el formado por dos lados consecutivos.
Ángulo interior =180° − Ángulo central
Ángulo interior del pentágono regular = 180° − 72º = 108º
Ángulo exterior de un polígono regular
Es el formado por un lado y la prolongación de un lado consecutivo.
Los ángulos exteriores e interiores son suplementarios, es decir, que suman 180º.
Ángulo exterior = Ángulo central
Ángulo exterior del pentágono regular = 72°
Si observas bien la figura, verás que puedes hallar el área
del polígono sumando
las áreas de
los triángulos iguales.

1Un campo rectangular tiene 170 m de base y 28 m de altura. Calcular:1Las hectáreas que tiene.2El precio del campo si el metro cuadrado cuesta 15 €.
2 Calcula el número de baldosas cuadradas, de 10 cm, de lado que se necesitan para enlosar una superficie rectangular de 4 m de base y 3 m de altura
.3Hallar el área de un triángulo rectángulo isósceles cuyos lados miden 10 cm cada uno.
4El perímetro de un triángulo equilátero mide 0.9 dm y la altura mide 25.95 cm. Calcula el área del triángulo.
5Calcula el número de árboles que pueden plantarse en un terreno rectangular de 32 m de largo y 30 m de ancho si cada planta necesita para desarrollarse 4 m²
6El área de un trapecio es 120 m², la altura 8 m, y la base menor mide 10 m. ¿Cuánto mide la otra base?
7Calcular el área de un paralelogramo cuya altura mide 2 cm y su base mide 3 veces más que su altura.
8Calcula el área de un rombo cuya diagonal mayor mide 10 cm y cuya diagonal menor es la mitad de la mayor.
9En el centro de un jardín cuadrado de 150 m de lado hay una piscina también cuadrada, de 25 m de largo. Calcula el área del jardín
10Calcula el área del cuadrado que resulta de unir los puntos medios de los lados de un rectángulo cuya base y altura miden 8 y 6 cm.
11Cuánto vale el área de la parte subrayada de la figura, si el área del hexágono es de 96 cm².
12Una zona boscosa tiene forma de trapecio, cuyas bases miden 128 m y 92 m. La anchura de la zona mide 40 m. Se construye un paseo de 4 m de ancho perpendicular a las dos bases. Calcula el área de la zona arbolada que queda.
13Un jardín rectangular tiene por dimensiones 30 m y 20 m. El jardín está atravesado por dos caminos perpendiculares que forman una cruz. Uno tiene un ancho de 8 dm y el otro 7 dm. Calcula el área del jardín.
14Dado el cuadrado ABCD, de 4 m de lado, se une E, punto medio del segmento BC, con el vértice D. Calcular el área del trapecio formado.
15Calcula la cantidad de pintura necesaria para pintar la fachada de este edificio sabiendo que se gastan 0.5 kg de pintura por m2.

16Hallar el perímetro y el área de la figura:

Elige la respuesta correcta:
a) ¿Cuál es el menor número de lados de un polígono para
que pueda descomponerse en triángulos?
- 20
- 5
- 4
- 3
b) La suma de los ángulos
interiores de un heptágono es:
- 360°
- 1080°
- 720°
- 900°
c) El ángulo central de un
eneágono regular mide:
- 20°
- 40°
- 50°
- 140°
d) Cada uno de los ángulos
interiores de un octógono mide:
- 40°
- 135°
- 120°
- 80°
e) ¿Cuál es el único polígono
regular que se descompone en triángulos equiláteros?
- Cuadrado.
- Hexágono.
- Octógono.
- Todos
los polígonos regulares.
f) ¿Se pueden inscribir los
polígonos en una circunferencia?
- Sólo
los cuadrados.
- Sólo
los hexágonos.
- Sólo
los regulares.
- No.
g) ¿Cuánto mide el ángulo
central de un triángulo equilatero?
- 120°
- Los
triángulos no tienen ángulos centrales.
- 180°
- 60°
h) ¿Cuál es el área de un
pentágono regular de 6 cm de lado y 4 cm de apotema?
- 120
cm2
- 30
cm2
- 60
cm2
- 240
cm2
Áreas de polígonos regulares
Para calcular el área de un polígono regular
cualquiera se divide en triángulos uniendo el centro
con cada uno de los vértices. La altura de cada uno
de los triángulos coincide con la apotema del
polígono. Se calcula el área de uno de estos
triángulos y se multiplica por el número de triángulos
que se han formado.
Perímetro de un polígono regular
El perímetro es igual al número de lados por la longitud del lado.
P = n · l
Áreas de polígonos irregulares
Para calcular el área de un polígono irregular
cualquiera debemos basarnos en métodos indirectos.
Estos métodos, básicamente, son tres: el llamado
método de triangulación, el uso de una trama
cuadriculada o, en algunos casos, descomponer el
polígono en cuadriláteros conocidos.
Perímetro de un polígono irregular
El perímetro es igual a la suma de las longitudes de los lados.
BLOQUE V
Empleas la circunferencia
Circunferencia
La circunferencia es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro.

RECTAS Y SEGMENTOS EN LA CIRCUNFERENCIA
Para poder hablar de rectas y segmentos en la circunferencia primero se maneja el concepto de circunferencia que es el conjunto de todos los puntos de un plano que equidistan de otro punto llamado centro.Las rectas y segmentos de la circunferencia son: radio, diámetro, cuerda, tangente, secante y arco mismos que se apreciarán y distinguirán con el apoyo de GEOGEBRA y para esto se debe dar clic en la liga RECTAS Y SEGMENTOS EN LA CIRCUNFERENCIA que se encuentra en la parte inferior de la siguiente imagen .
Al trabajar las rectas y segmentos en la circunferencia hay que tener presente los siguientes teoremas:
- El diámetro divide a la circunferencia y al círculo en dos partes iguales.
- El diámetro es la mayor cuerda de la circunferencia.
- · En una circunferencia, o en circunferencias iguales, a cuerdas iguales corresponden arcos iguales, y si dos cuerdas son desiguales, a la mayor corresponde mayor arco.
- · La tangente a una circunferencia es perpendicular al radio en el punto de contacto.
También se podrán conocer conceptos de geometría tales como los ángulos de una circunferencia los cuales son: ángulo central, inscrito, semiinscrito, interior, exterior y circunscrito, sus definiciones y se trabajaron en GEOGEBRA y para conocerlas se debe dar clic en la liga corresponde a la imagen.
- MEDIDA DE UN ÁNGULO INSCRITO. La medida de todo ángulo inscrito es igual a la mitad del arco comprendido entre sus lados.
- MEDIDA DE UN ÁNGULO SEMIINSCRITO: La medida del ángulo semiinscrito es igual a la mitad del arco comprendido entre sus lados.
- MEDIDA DEL ÁNGULO INTERIOR. la medida del ángulo interior es igual a la semisuma de las medidas de los arcos comprendidos por sus lados y por sus prolongaciones.
- MEDIDA DEL ÁNGULO EXTERIOR: La medida del ángulo exterior es igual a la semidiferencia de las medida de los arcos comprendidos por sus lados.
Ángulos
LOS ÁNGULOS EN LA CIRCUNFERENCIA
Podemos dibujar ángulos que se relacionen con la circunferencia. Según la posición que ocupen reciben nombres apropiados con relación a esa posición.
Cuanto se refiere a los ÁNGULOS en la circunferencia, siempre RELACIONAMOS a éstos con los ARCOS que forman.
1) Ángulo central: nos hemos referido a él en más de una ocasión; se trata del ángulo formado por dos radios que son sus lados y su vértice se encuentra en el centro O de la circunferencia.
En la figura siguiente ves que el arco  corresponde al ángulo central Ô que lo representamos con el acento circunflejo
corresponde al ángulo central Ô que lo representamos con el acento circunflejo  sobre la letra que representa el vértice del ángulo.
sobre la letra que representa el vértice del ángulo.
 El arco
El arco  corresponde al ángulo central
corresponde al ángulo central  o lo que es lo mismo, la longitud del arco comprendido entre sus lados (los radios) pertenece al ángulo central
o lo que es lo mismo, la longitud del arco comprendido entre sus lados (los radios) pertenece al ángulo central  y su medida es de 96º.
y su medida es de 96º.
Cuanto mayor es el ángulo central mayor será la longitud del arco que abarcan sus lados:
 Vas a tener en cuenta que cuando representamos con letras un ángulo, por ejemplo
Vas a tener en cuenta que cuando representamos con letras un ángulo, por ejemplo  significa que la letra señalada con
significa que la letra señalada con  en este caso la O, nos referimos a que el vértice del ángulo se encuentra en dicha letra.
Cuando nos refiramos a un arco entre dos puntos señalados con letras, por ejemplo: el arco entre los puntos A y B lo representamos:
en este caso la O, nos referimos a que el vértice del ángulo se encuentra en dicha letra.
Cuando nos refiramos a un arco entre dos puntos señalados con letras, por ejemplo: el arco entre los puntos A y B lo representamos:  Las dos circunferencias de la última figura de igual radio, la longitud del arco vemos que están en razón directa con la medida del ángulo central: a mayor medida del ángulo central corresponde mayor longitud de arco. La longitud
Las dos circunferencias de la última figura de igual radio, la longitud del arco vemos que están en razón directa con la medida del ángulo central: a mayor medida del ángulo central corresponde mayor longitud de arco. La longitud  es decir, a 50º corresponde el arco
es decir, a 50º corresponde el arco  y a 111º corresponde
y a 111º corresponde  y puedes comprobar que a mayor ángulo central corresponde mayor longitud de arco.
y puedes comprobar que a mayor ángulo central corresponde mayor longitud de arco.
Muchas veces cuando nos referimos a las medidas de los arcosde la circunferencia hablamos de lo que miden sus longitudes en: m., dm., cm., pero también podemos referirnos a su medida en grados, minutos y segundos, incluso en radianes.
Cuando decimos que un arco mide 75º12’13’’ quiere decir que su ángulo entral tiene la misma medida.
Las medidas de los arcos de la última figura puedes expresarlos también en grados: el arco  mide 50º y arco
mide 50º y arco  111º.
111º.
Las medidas de los ángulos y arcos de una circunferencia se miden en grados, minutos y segundos.
15.144 Una circunferencia tiene un radio de 5 m. ¿Cuánto mide un arco de esta circunferencia que corresponde a un ángulo central 60º?
Respuesta: 5,23 m.
Solución:
La longitud total de la circunferencia  m., corresponde a 380º
m., corresponde a 380º
Una longitud de………………………..X m. corresponden a 60º
 15.145 ¿Cuál es la longitud de un arco en metros sabiendo que su ángulo central vale 65º y su radio 8 m.?
Respuesta: 9,07 m.
2) Ángulo inscrito: es el ángulo que tiene su vértice en un punto de la misma línea de la circunferencia y sus lados la cortan.
15.145 ¿Cuál es la longitud de un arco en metros sabiendo que su ángulo central vale 65º y su radio 8 m.?
Respuesta: 9,07 m.
2) Ángulo inscrito: es el ángulo que tiene su vértice en un punto de la misma línea de la circunferencia y sus lados la cortan.
 Ves que el vértice se encuentra en el punto P de la circunferencia y los lados del ángulo inscrito cortan a la circunferencia en A y en B.
¿Cuál es la medida del arco correspondiente a este ángulo inscrito de 44º? Por supuesto que no se trata de la longitud del arco
Ves que el vértice se encuentra en el punto P de la circunferencia y los lados del ángulo inscrito cortan a la circunferencia en A y en B.
¿Cuál es la medida del arco correspondiente a este ángulo inscrito de 44º? Por supuesto que no se trata de la longitud del arco  por que el ángulo tendría que ser central.
por que el ángulo tendría que ser central.
Modo de calcular el valor de un ángulo inscrito:
En primer lugar trazo una línea que une el punto B con el centroO, tal como lo puedes ver en la figura siguiente:
 El segmento OB y el segmento OP son iguales por tratarse del radio. Esto quiere decir que si los lados con vértice en O son iguales, los ángulos cuyos vértices están en B y en P serán iguales.
El segmento OB y el segmento OP son iguales por tratarse del radio. Esto quiere decir que si los lados con vértice en O son iguales, los ángulos cuyos vértices están en B y en P serán iguales.
Las medidas de estos ángulos los tienes a continuación y comprobamos que tienen 44º:
 Ahora observa bien la figura siguiente que como estudiamos con anterioridad e hicimos la demostración correspondiente sobre elvalor de un ángulo exterior de un triángulo, decíamos que eraigual a la suma de los otros dos ángulos interiores no adyacentes:
Ahora observa bien la figura siguiente que como estudiamos con anterioridad e hicimos la demostración correspondiente sobre elvalor de un ángulo exterior de un triángulo, decíamos que eraigual a la suma de los otros dos ángulos interiores no adyacentes:
 El ángulo con vértice en O es igual a los valores de los ángulos cuyos vértices están en B y en P, podríamos escribir:
El ángulo con vértice en O es igual a los valores de los ángulos cuyos vértices están en B y en P, podríamos escribir:  Vemos que los ángulos
Vemos que los ángulos  ambos valen en nuestro ejemplo 44º.
La igualdad
ambos valen en nuestro ejemplo 44º.
La igualdad  podemos escribirla
podemos escribirla  por ser iguales los ángulos
por ser iguales los ángulos  Esto quiere decir que
Esto quiere decir que  podemos escribir:
podemos escribir:  y de esta igualdad despejamos
y de esta igualdad despejamos  :
:

Comprobamos que el ángulo central en  vale 88º, es decir, el doble que los ángulos inscritos
vale 88º, es decir, el doble que los ángulos inscritos  y abarca el arco
y abarca el arco  Esto significa que la medida del arco que abarca el ángulo
Esto significa que la medida del arco que abarca el ángulo  o el ángulo
o el ángulo  valdrán la mitad de lo que abarca el ángulo central
valdrán la mitad de lo que abarca el ángulo central  ,es decir,
,es decir,  .
El valor de un ángulo inscrito es igual a la mitad del ángulo central, luego, la medida del arco correspondiente a un ángulo inscrito equivale a la mitad del arco que comprenden sus lados o a la mitad del ángulo central correspondiente.
.
El valor de un ángulo inscrito es igual a la mitad del ángulo central, luego, la medida del arco correspondiente a un ángulo inscrito equivale a la mitad del arco que comprenden sus lados o a la mitad del ángulo central correspondiente.
3) Ángulo semi-inscrito: El ángulo semi-inscrito es el que su vértice se encuentra en un punto de la circunferencia, y sus lados, uno es tangente y el otro secante con relación a la circunferencia:
 En la figura siguiente señalamos el centro y creamos el ángulo central
En la figura siguiente señalamos el centro y creamos el ángulo central  . El lado
. El lado  del ángulo central es perpendicular allado secante
del ángulo central es perpendicular allado secante  . El lado
. El lado  del ángulo central es perpendicular al lado tangente
del ángulo central es perpendicular al lado tangente  :
:
 Pasamos a la figura siguiente y puedes ver que hemos creado los ángulos
Pasamos a la figura siguiente y puedes ver que hemos creado los ángulos  que abarca el arco
que abarca el arco  y
y  que abarca el arco
que abarca el arco  , es decir, los ángulos en
, es decir, los ángulos en  y en
y en  . Estos ángulos son iguales (en este caso miden 46º) porque sus lados son perpendiculares:
. Estos ángulos son iguales (en este caso miden 46º) porque sus lados son perpendiculares:

 El arco
El arco  corresponde al ángulo central
corresponde al ángulo central  de 46º. Podemos escribir:
de 46º. Podemos escribir:
 Como el valor del arco correspondiente al ángulo central es el que abarcan sus lados escribimos:
Como el valor del arco correspondiente al ángulo central es el que abarcan sus lados escribimos:
 También podemos decir que:
También podemos decir que:
 debido a que OD es mediatriz de CE.
Como el arco
debido a que OD es mediatriz de CE.
Como el arco  es la mitad del arco
es la mitad del arco  podemos escribir:
podemos escribir:
 Como
Como  , podemos decir que también:
, podemos decir que también: Si ahora sustituyes :
Si ahora sustituyes :
 tenemos la igualdad :
tenemos la igualdad :  La medida de un ángulo semi-inscrito es igual a la mitad del arco que abarcan los lados.
La medida de un ángulo semi-inscrito es igual a la mitad del arco que abarcan los lados.
Todo lo explicado sobre el ángulo semi-inscrito lo puedes ver en el gráfico siguiente:
 Sucede como si se tratara de un ángulo inscrito. Comprobamosque la medida del ángulo semi-inscrito equivale a la mitad del ángulo central y es igual, a la mitad de la medida del arco que abarcan sus lados.
Sucede como si se tratara de un ángulo inscrito. Comprobamosque la medida del ángulo semi-inscrito equivale a la mitad del ángulo central y es igual, a la mitad de la medida del arco que abarcan sus lados.
Perimetro y Area
perimetro de una circunferencia
El perímetro de un círculo, puede ser denotado por la literal “P”. De esta manera, la ecuación para hallar el valor de P es:
P = (pi)*(d),
donde:
pi = 3.1415…
d = diámetro del círculo.
NOTA: Usualmente el valor de pi se redondea a 3.15.
ÁREA DEL CÍRCULO
El área de un circulo es igual al valor de su radio elevado al cuadrado multiplicado por Π.
Se llama Π= Pi al valor del cociente de la longitud de una circunferencia entre su diámetro. Su valor aproximado es 3,14. En realidad Π tiene infinitos decimales.
ejercicios
Ejemplo 1
1.Encuentre la ecuación de la circunferencia de centro en C(-3, 2) y radio 6.
....
SOLUCIÓN
En este caso: h = -3, k = 2 y r = 6. Al sustituir estos valores en la ecuación (1) de la sección 5.1., se obtiene:

Al desarrollar los binomios en la última igualdad y simplificar, se obtiene finalmente:

Ejemplo 2
2.Hallar la ecuación de la circunferencia que pasa por el origen y tiene su centro en el punto común a las rectas:  y
y .
.
..
..
SOLUCIÓN
Al resolver simultáneamente el sistema:  se obtiene
se obtiene  . Asi que el centro de la circunferencia es el punto C(3, 1).
. Asi que el centro de la circunferencia es el punto C(3, 1).

Ahora, como la circunferencia pasa por el punto 0(0, 0), se tiene que  es el valor del radio.
es el valor del radio.
Usando nuevamente la ecuación (1) de la sección 5.1. con  y
y  , se obtiene:
, se obtiene:

..
Ejemplo 3
3.Determine la ecuación de la circunferencia uno de cuyos diámetros es el segmento de extremos  y
y  .
.
......
SOLUCIÓN
Si D denota el diámetro de la circunferencia, entonces, el radio r es  .
.
Es decir,  (fórmula de la distancia).
(fórmula de la distancia).
Esto es, 
Ahora, las coordenadas del centro C(h, k) son las coordenadas del punto medio del segmento  . (Ver fig.).
. (Ver fig.).
Asi que:  y
y 
Luego, la ecuación de la circunferencia pedida es:  .
.
Ejemplo 4
4.La ecuación:  representa una circunferencia. Determine su centro C(h, k) y su radio r.
representa una circunferencia. Determine su centro C(h, k) y su radio r.
....
..
SOLUCIÓN
La ecuación dada puede escribirse en las formas equivalentes: 


Comparando esta última ecuación con la ecuación (1) de la sección 5.1., se deduce que:  y
y  .
.
Luego, el centro de la circunferencia es el punto C(-3, 7) y su radio es r = 8.
Ejemplo 5
5.Hallar la ecuación de la circunferencia que pasa por los puntos A(0, 6), B(4, -2) y C(9, 3). Encuentre las coordenadas del centro y el radio.
....
....
SOLUCIÓN
Como A, B yC no están alineados, hay una circunferencia ð que pasa por A, B y C.
Su ecuación es la forma

x2 + y2 + 2dx + 2ey + f = 0
Hallemos d, e y f. Como A(0, 6) Î C ,
02 + 62 + 2d.0 + 2e.6 + f = 0
Asi que: 36 + 12e + f = 0 (1)
Como B(4, -2) Î C , 16 + 4 + 2d.4 + 2e.(-2) + f = 0
Es decir, 20 + 8d – 4e + f = 0 (2)
Como C(9, 3) Î C , 81 + 9 + 2d.9 + 2e.3 + f = 0
Asi que: 90 + 18d + 6e + f = 0 (3)
El sistema de ecuaciones (1), (2), (3) puede escribirse así:
12e + f = -36
8d – 4e + f = -20
18d + 6e + f = -90
o también:

 cuya solución es: d = -4, e = -3, f = 0
cuya solución es: d = -4, e = -3, f = 0
Luego la ecuación de ð es : x2 + y2 – 8x – 6y = 0 que podemos escribir:
(x2 – 8x + 16) + (y2 – 6y + 9) = 25
ó (x – 4)2 + (y – 3)2 = 25
Así que la circunferencia C circunscrita al triángulo ABC tiene centro en (4, 3) y radio 5.
..
Ejercicio 6
6.Determine los puntos comunes a la circunferencia  y a la recta
y a la recta  .
.
..
Ejercicio 7
7.Determine los puntos comunes a la circunferencia  y a la recta
y a la recta  .
.
..
..
SOLUCIÓN
Como en el caso anterior, los puntos comunes son las soluciones al sistema de ecuaciones:
 (1)
(1)
 (2)
(2)
De (2) se tiene:  (3).
(3).
Sustituyendo (3) en (1) se puede escribir:

La última ecuación, tiene como única solución x = 2 que corresponde a la abscisa del único punto de intersección.
Sustituyendo el valor de x = 2 en (3) se obtiene:  . De esta forma
. De esta forma  es el único punto común a la recta y a la circunferencia.
es el único punto común a la recta y a la circunferencia.
En este caso, la recta es tangente a la circunferencia en el punto  .
.
La figura adjunta ilustra la situación.

BLOQUE VI
Describes las Relaciones Trigonométricas
Para las Funciones Trigonométricas, como se mencionó anteriormente,
haremos uso del Teorema de Pitágoras y trabajaremos con las Funciones
de Seno, Coseno y Tangente, y sus inversas, además de apoyarnos
siempre con la Calculadora.

Las letras minúsculas son las que utilizamos en el Teorema de Pitágoras,
las letras Mayúsculas, en éste caso, se utilizarán para referirnos a los
Ángulos del Triángulo.
Empezaremos a ver cada una de las Funciones:
1. Función Seno ( Sen):
La Función Seno nos describe la relación existente entre Lado Opuesto sobre la
Hipotenusa. Su simbología es la siguiente:

2. Función Coseno ( Cos):
La Función Coseno describe la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:

3. Función Tangente ( Tan):
Ésta Función nos representa la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:

También tenemos las Funciones que son inversas a las anteriores:
4. Función Cotangente ( Cot):
Que describe la relación entre Lado Adyacente con Lado Opuesto:

5. Función Secante ( Sec):
Relación entre Hipotenusa sobre Lado Adyacente:

6. Función Cosecante ( CsC):
Nos muestra la relación entre Hipotenusa sobre Lado Opuesto:

Sistema Sexagesimal y Circular
El sistema sexagesimal es un sistema de numeración en el que cada unidad se divide en 60
unidades de orden inferior, es decir, es su sistema de numeración en base 60.
Se aplica en la actualidad a la medida del tiempo y a la de la amplitud de
los ángulos. 1 h 60 min 60 s 1º 60' 60''El sistema circular. En este sistema se usa como unidad el ángulo llamado
"radián". Un radián, es el ángulo cuyos lados comprenden un arco a la
circunferencia cuya longitud es igual al radio de la circunferencia. Un pi
radián equivale a 180° Para encontrar la medición de cualquier ángulo utilizamos
el transportador, que usualmente está dividido en 360 partes iguales y cada una
de esas partes equivalen a un grado, es decir, está en el sistema
sexagesimal.
Razones trigonométricas directas y recíprocas del triángulo rectángulo:
Ya conocidas las tres funciones trigonométricas, (seno, coseno & tangente) en base a
ellas nacen tres funciones recíprocas (cosecante, secante & cotangente)
que, se podría decir, que son los datos invertidos de cada función:
Funciones
(razones) trigonométricas
Directas
Recíprocas
sen
seno
cosec
(csc)
cosecante
cos
coseno
sec
secante
tan
(tg)
tangente
cotan
(cotg)
cotangente
Cálculo de las razones trigonométricas de los ángulos de 30° 45° & 60°
Si dibujamos un triángulo equilátero ABC, cada uno de sus tres ángulos mide 60º y, si trazamos una altura del mismo, h, el ángulo del vértice A por el que la hemos trazado queda dividido en dos iguales de 30º cada uno. Recurriendo al Teorema de Pitágoras, tenemos que la altura es: La raíz cuadrada de la suma de los dos catetos al cuadrado.
Resolución de triángulos rectángulos
En toda aplicación para la resolución de triángulos se proporcionan datos incompletos o se desconocen algunos de ellos, como en el caso de los ángulos o longitudes de catetos de un triángulo rectángulo. Al procedimiento de encontrar los valores restantes partiendo de los datos originales, se le conoce como "Resolución de un triángulo rectángulo" Para que esto se cumpla, debes resolver problemas sencillos donde apliques las razones trigonométricas para el uso de triángulos rectángulos y recordar el teorema de Pitágoras.
Resolver un triángulo es hallar sus lados, ángulos y área. Es necesario conocer dos lados del triángulo, o bien un lado y un ángulo distinto del recto.
1. Se conocen la hipotenusa y un cateto




Resolver el triángulo conociendo:
2. Se conocen los dos catetos



 Resolver el triángulo conociendo:
Resolver el triángulo conociendo:
3. Se conocen la hipotenusa y un ángulo agudo




Resolver el triángulo conociendo:
Ejercicios
1 Expresa en grados sexagesimales los siguientes ángulos:
1 3 rad
22π/5rad.
33π/10 rad.
2 Expresa en radianes los siguientes ángulos:
1316°
2 10°
3 127º
3 Sabiendo que cos α = ¼ , y que 270º <α <360°. Calcular las restantes razones trigonométricas del ángulo α.
4 Sabiendo que tg α = 2, y que 180º < α <270°. Calcular las restantes razones trigonométricas del ángulo α.
5 Sabiendo que sec α = 2, 0< α <  /2, calcular las restantes razones trigonométricas.
/2, calcular las restantes razones trigonométricas.
6 Calcula las razones de los siguientes ángulos:
1225°
2 330°
3 2655°
4 −840º
7Comprobar las identidades:
1 2
2 3
3 4
4 5
5 8 De un triángulo rectángulo ABC, se conocen a = 5 m y B = 41.7°. Resolver el triángulo
8 De un triángulo rectángulo ABC, se conocen a = 5 m y B = 41.7°. Resolver el triángulo
9De un triángulo rectángulo ABC, se conocen b = 3 m y B = 54.6°. Resolver el triángulo.
10De un triángulo rectángulo ABC, se conocen a = 6 m y b = 4 m. Resolver el triángulo.
11De un triángulo rectángulo ABC, se conocen b = 3 m y c = 5 m. Resolver el triángulo.
12Un árbol de 50 m de alto proyecta una sombra de 60 m de larga. Encontrar el ángulo de elevación del sol en ese momento.
13Un dirigible que está volando a 800 m de altura, distingue un pueblo con un ángulo de depresión de 12°. ¿A qué distancia del pueblo se halla?
14Hallar el radio de una circunferencia sabiendo que una cuerda de 24.6 m tiene como arco correspondiente uno de 70°
15Calcular el área de una parcela triangular, sabiendo que dos de sus lados miden 80 m y 130 m, y forman entre ellos un ángulo de 70°.
16 Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa bajo un ángulo de 30° y si nos acercamos 10 m, bajo un ángulo de 60°.
17 La longitud del lado de un octógono regular es 12 m. Hallar los radios de la circunferencia inscrita y circunscrita.
BLOQUE VII
Aplicas las funciones trigonométricas
Funciones trigonométricas en el plano cartesiano: De acuerdo con el cuadrante en que se halle el lado terminal del ángulo y teniendo en cuenta que la distancia de un punto cualquiera al origen de coordenadas es siempre positiva, y aplicando la "ley de los signos", las funciones trigonométricas pueden ser positivas o negativas.
Sen(x) positivo en cuadrantes I y II porque en ambos el cateto opuesto es positivo.
Sen(x) negativo en cuadrantes III y IV porque en ambos el cateto opuesto es negativo.
Cos(x) positivo en cuadrantes I y IV porque en ambos el cateto ayacente es positivo.
Cos(x) negativo en cuadrantes II y III porque en ambos el cateto adyacente es negativo.
Tan(x) positivo en cuadrantes I y III porque ambos catetos tienen igual signo
Tan(x) negativo en cuadrantes II y IV porque ambos catetos tienen distintos signos
seno
coseno
tangente
cotangente
secante
cosecante
I
+
+
+
+
+
+
II
+
-
-
-
-
+
III
-
-
+
+
-
-
IV
-
+
-
-
+
-
Círculo unitario
Cuando se incorpora un círculo de radio =1, aun sistema de referencia coordenado cartesiano, de tal manera que el centro del círculo coincide con el origen de coordenadas, se tiene una figura que recibe el nombre de círculo unitario.
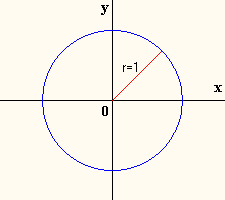
Las funciones circulares que estudiaremos se basan en una función cuyo dominio es el conjunto de los números reales y el recorrido es el conjunto de puntos del círculo unitario. El círculo unitario es un círculo de radio 1 con centro en el origen del sistema de coordenadas, esto es, el punto (0,0) y su ecuación es x2 + y2 = 1.
Como el radio del círculo unitario es 1, entonces la circunferencia del círculo es:

Así que un cuarto, una mitad y tres cuartos de la circunferencia son respectivamente:

De manera que, los puntos circulares correspondientes en los ejes coordenados son:
Nota: Observa que las coordenadas de los puntos circulares P(0) y P(2p) son iguales.


Gráficas de las funciones seno, coseno y tangente
Consideramos como “Gráficas de las funciones (Seno, Coseno, Tangente)” al comportamiento que van presentando dichas funciones previamente mencionadas a través del recorrido de un conjunto de valores entrantes llamado así mismo (Dominio) y su conjunto de valores de salientes (Rango).
*Gráfica de la función seno: y = sen x
Justamente de los valores que arroge la tabla una a una es construida las coordenadas por los elementos (X, F(X)) y es empleada de tal manera que X indica la cantidad de unidad a avanzar en el eje “X” hacia la derecha o izquierda dependiendo de su valor (Positivo o Negativo) de igual manera F(X) indica la cantidad de unidad a avanzar en el eje “y” hacia la arriba o abajo dependiendo de su valor (Positivo o Negativo) estableciendo el punto que represente la coordenada.

Justamente de los valores que arroge la tabla una a una es construida las coordenadas por los elementos (X, F(X)) y es empleada de tal manera que X indica la cantidad de unidad a avanzar en el eje “X” hacia la derecha o izquierda dependiendo de su valor (Positivo o Negativo) de igual manera F(X) indica la cantidad de unidad a avanzar en el eje “y” hacia la arriba o abajo dependiendo de su valor (Positivo o Negativo) estableciendo el punto que represente la coordenada.
Función seno
f(x) = sen x

Dominio: 
Recorrido: [−1, 1]
Período: 
Continuidad: Continua en 
Impar: sen(−x) = −sen x
f(x) = cos x

Dominio: 
Recorrido: [−1, 1]
Período: 
Continuidad: Continua en 
Par: cos(−x) = cos x
Función tangente
f(x) = tg x

Dominio: 
Recorrido: 
Continuidad: Continua en 
Período: 
Impar: tg(−x) = −tg x
Función cotangente
f(x) = cotg x

Dominio:
Recorrido: 
Continuidad: Continua en 
Período: 
Impar: cotg(−x) = −cotg x
Función secante
f(x) = sec x

Dominio: 
Recorrido: (− ∞, −1]  [1, ∞)
[1, ∞)
Período: 
Continuidad: Continua en 
Par: sec(−x) = sec x
Función cosecante
f(x) = cosec x

Dominio: 
Recorrido: (− ∞, −1]  [1, ∞)
[1, ∞)
Período: 
Continuidad: Continua en 
Impar: cosec(−x) = −cosec x
BLOQUE VIII
Aplicas las leyes de los senos y cosenos
Ley de los senos
La ley de los senos es la relación entre los lados y ángulos de triángulos no rectángulos (oblicuos). Simplemente, establece que la relación de la longitud de un lado de un triángulo al seno del ángulo opuesto a ese lado es igual para todos los lados y ángulos en un triángulo dado.
En ∆ABC es un triángulo oblicuo con lados a, b y c, entonces  .
.

Para usar la ley de los senos necesita conocer ya sea dos ángulos y un lado del triángulo (AAL o ALA) o dos lados y un ángulo opuesto de uno de ellos (LLA). Dese cuenta que para el primero de los dos casos usamos las mismas partes que utilizó para probar la congruencia de triángulos en geometría pero en el segundo caso no podríamos probar los triángulos congruentes dadas esas partes. Esto es porque las partes faltantes podrían ser de diferentes tamaños. Esto es llamado el caso ambiguo y lo discutiremos más adelante.
ejercicios
Ejemplo 1: Dado dos ángulos y un lado no incluído (AAL).
Dado ∆ABC con A = 30°, B = 20° y a = 45 m. Encuentre el ángulo y los lados faltantes.
 El tercer ángulo del triángulo es C = 180° – A – B = 180° – 30° – 20 ° = 130° Por la ley de los senos,
El tercer ángulo del triángulo es C = 180° – A – B = 180° – 30° – 20 ° = 130° Por la ley de los senos,  Por las propiedades de las proporciones
Por las propiedades de las proporciones  Ejemplo 2: Dado dos ángulos y un lado incluído (ALA).
Dado A = 42°, B = 75° y c = 22 cm. Encuentre el ángulo y los lados faltantes.
Ejemplo 2: Dado dos ángulos y un lado incluído (ALA).
Dado A = 42°, B = 75° y c = 22 cm. Encuentre el ángulo y los lados faltantes.
 El tercer ángulo del triángulo es: C = 180° – A – B = 180° – 42° – 75° = 63° Por la ley de los senos,
El tercer ángulo del triángulo es: C = 180° – A – B = 180° – 42° – 75° = 63° Por la ley de los senos,

Por las propiedades de las proporciones  y
y 
El caso ambiguo
Si dos lados y un ángulo opuesto a uno de ellos es dado, tres posibilidades pueden ocurrir.
(1) No existe tal triángulo.
(2) Dos triángulos diferentes existen.
(3) Exactamente un triángulo existe.
Considere un triángulo en el cual se le da a, b y A. (La altitud h del vértice B al lado  , por la definición de los senos es igual a b sin A.)
, por la definición de los senos es igual a b sin A.)
(1) No existe tal triángulo si A es agudo y a < h o A es obtuso y a ≤ b.

(2) Dos triángulos diferentes existen si A es agudo y h < a < b.

(3) En cualquier otro caso, exactamente un triángulo existe.

Ejemplo 1: No existe solución
Dado a = 15, b = 25 y A = 80°. Encuentre los otros ángulos y el lado.
h = b sin A = 25 sin 80° ≈ 24.6  Dese cuenta que a < h. Así parece que no hay solución. Verifique esto usando la ley de los senos.
Dese cuenta que a < h. Así parece que no hay solución. Verifique esto usando la ley de los senos.


Esto contrae el hecho de que –1 ≤ sin B ≤ 1. Por lo tanto, no existe el triángulo.
Ejemplo 2: Dos soluciones existen
Dado a = 6. b = 7 y A = 30°. Encuentre los otros ángulos y el lado.
h = b sin A = 7 sin 30° = 3.5 h < a < b por lo tanto, hay dos triángulos posibles.  Por la ley de lo senos,
Por la ley de lo senos, 

Hay dos ángulos entre 0° y 180° cuyo seno es aproximadamente 0.5833, 35.69° y 144.31°.
Si B ≈ 35.69° Si B ≈ 144.31°
C ≈180° – 30° – 35.69° ≈ 114.31° C ≈ 180° – 30° – 144.31° ≈ 5.69°

Ejemplo 3: Una solución existe
Dado a = 22, b =12 y A = 40°. Encuentre los otros ángulos y el lado.
a > b  Por la ley de lo senos,
Por la ley de lo senos, 

B es agudo.
C ≈ 180° – 40° – 20.52° ≈ 119.48°
Por la ley de lo senos,

Si se nos dan dos lados y un ángulo incluído de un triángulo o si se nos dan 3 lados de un triángulo, no podemos usar la ley de los senos porque no podemos establecer ninguna proporción donde información suficiente sea conocida. En estos dos casos debemos usar la ley de los cosenos.
Encuentra la medida del lado b para el triángulo ABC según demostrado en la siguiente figura:

Estrategia para resolver el ejercicio:
Determina los datos:
a=10m
A=30°
B =40°
b = ?
Utiliza la siguiente ecuación:

Despeja para la desconocida:

Reemplaza los valores conocidos en la ley del seno
Usa una calculadora o una tabla trigonométrica para ir desde el seno de A hasta obtener la medida del ángulo A segúndemostrado:

La respuesta es: el ángulo obtenido es b=13m
Ley de los cosenos
La ley de los cosenos es usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la ley de los senos porque no podemos establecer una proporción que pueda resolverse.
La ley de los cosenos establece:
c2 = a2 + b2 – 2abcos C.
Esto se parece al teorema de Pitágoras excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras. Así, el teorema de Pitágoras es un caso especial de la ley de los cosenos.
La ley de los cosenos también puede establecerse como
b2 = a2 + c2 – 2accos B or
a2 = b2 + c2 – 2bccos A.
ejercicios
Ejemplo 1: Dos lados y el ángulo incluído-LAL
Dado a = 11, b = 5 y C = 20°. Encuentre el lado y ángulos faltantes.


Para encontrar los ángulos faltantes, ahora es más fácil usar la ley de los senos.

Ejemplo 2: Tres lados-LLL
Dado a = 8, b = 19 y c = 14. Encuentre las medidas de los ángulos.

Es mejor encontrar el ángulo opuesto al lado más grande primero. En este caso, ese es el lado b.

Ya que el cos B es negativo, sabemos que B es un ángulo obtuso.
B ≈ 116.80°
Ya que B es un ángulo obtuso y un triángulo tiene a lo más un ángulo obtuso, sabemos que el ángulo A y el ángulo C ambos son agudos.
Para encontrar los otros dos ángulos, es más sencillo usar la ley de los senos.

BLOQUE IX
Aplicas la estadistica elemental
Poblacion
una población es un conjunto de individuos u objetos que poseen la característica que se desea estudiar. En un sentido más estadístico, una población es el conjunto de mediciones de una cierta característica en todos los individuos u objetos que poseen dicha característica.
Muestra
Es el conjunto de mediciones que han sido realmente recolectados. La extracción de la muestra es un paso bien importante porque es a partir de ella que se sacan conclusiones acerca de la población. Si el diseño es sencillo la muestra tiene que ser relativamente grande, alrededor de un 10% del tamaño de la población
medidas de tendencia central y de deprecion
A
veces, de los datos recolectados ya organizados en alguna de las formas
vistas en capítulos anteriores, se desea encontrar una especie de
punto central en función de sus frecuencias. En Estadística se
conocen tres diferentes, llamadas medidas de tendencia central, cuya
utilización varía de acuerdo con lo que se desee del conjunto de
datos recolectados. Esas tres medidas de tendencia central son la
media, la mediana y la moda.
a) Media aritmética: es la medida de tendencia
central conocida popularmente como “promedio” es el valor obtenido
al sumar todos los datos y dividir el resultado
entre el número total de datos.
 es
el símbolo de la media aritmética, también conocido como "equis barra".
es
el símbolo de la media aritmética, también conocido como "equis barra".
Ejemplo:
Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78 kg. Hallar el peso medio.

Esta es la media para datos no agrupados, pero para datos agrupados, es la siguiente:


 =media o promedio.
=media o promedio.
∑ f x = suma de las frecuencias por su correspondiente dato nominal.
n = suma de todas las frecuencias (número de datos recolectados).
Por ejemplo:
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la media.
xi fi xi · fi [10, 20) 15 1 15 [20, 30) 25 8 200 [30,40) 35 10 350 [40, 50) 45 9 405 [50, 60 55 8 440 [60,70) 65 4 260 [70, 80) 75 2 150 42 1 820

Para calcular la media, debe añadirse una columna fx a la tabla original en la que se registren los resultados correspondientes al producto de la frecuencia por su valor nominal (fx).
LA MEDIA PARA FRECUENCIAS POR INTERVALOS:
Cuando los datos recolectados han sido organizados en una tabla de frecuencias por intervalos,
la media para poblaciones como para muestras se puede calcular por medio de la fórmula
 en donde:
en donde:
 = media
x = punto medio del intervalo.
∑ f x = suma de las frecuencias por su correspondiente dato nominal.
n = suma de todas las frecuencias (número de datos recolectados). .
= media
x = punto medio del intervalo.
∑ f x = suma de las frecuencias por su correspondiente dato nominal.
n = suma de todas las frecuencias (número de datos recolectados). .
Obsérvese que es la misma fórmula que la correspondiente a los datos organizados en tablas de
distribución de frecuencias simples, en donde la única diferencia es la interpretación de la x. En una
representa el valor nominal, en ésta el punto medio del intervalo. De hecho, esta situación se va a
repetir en las otras dos medidas de tendencia central que faltan de estudiar aún, la mediana y la
moda, ya que también se estudiarán en dos casos: cuando los datos estén organizados en tablas con
frecuencias simples o cuando estén por intervalos.
Para calcular la media de datos organizados por intervalos, deben añadirse ahora dos columnas a la tabla original: laprimera columna añadida es para anotar el valor del puntomedio del intervalo (x) y la otra en la que se registren los resultados correspondientes al producto de la frecuencia por el correspondiente valor del punto medio del intervalo (fx).
Ejemplo 1: Calcular la media de los valores agrupados en intervalos de la tabla siguiente.
intervalos f
0 - 2 12
3 - 5 13
6 - 8 23
9 - 11 16
12 - 14 18
82
Solución: Deben añadirse a la tabla original dos columnas encabezadas por x y por fx, en donde
se anotarán los resultados correspondientes a los puntos medios de cada intervalo y al
producto de la frecuencia por ese punto medio.
La tabla completa con las cuatro columnas queda como se muestra abajo a continuación:
La suma de los valores de la columna fx es 619, de manera que utilizando la fórmula para el promedio, donde hay que recordar que , n =∑f se obtiene:
intervalos f punto medio x fx
0 - 2 12 1 12
3 - 5 13 4 52
6 - 8 23 7 161
9 - 11 16 10 160
12 - 14 18 13 234
82 619
 =619 /82=7 548
=619 /82=7 548
b) Moda: La moda es la medida de tendencia central que se define como aquel valor nominal que tiene la frecuencia mayor, es decir, la quese repite más veces. Por lo tanto, una distribución de frecuencias puede tener más de una moda o, inclusive, no tener moda cuando todos los datos tienen frecuencia 1.
Cuando los datos recolectados han sido organizados en una tabla de frecuencias simples, la moda
se obtiene buscando en la columna de frecuencias el o los valores que tengan mayor frecuencia. Es
exactamente lo mismo cuando están organizados por intervalos. La moda se simboliza con sus dos primeras iniciales: Mo
c)Mediana: La mediana es la medida de tendencia central que se define como aquel valor nominal que tiene,dentro de un conjunto de datos ordenados, arriba y abajo de él, el mismo número de datos nominales. En otras palabras, es el dato que está a la mitad, es el dato que divide en dos partes iguales a un
conjunto de datos.
Por ejemplo, del conjunto 3, 3, 3, 4, 5, 5, 5, 5, 5, 6, 6, 7, 8, 9, 9 el cinco remarcado en negrita
y subrayado es el que está a la mitad del conjunto ordenado, ya que antes de él existen 7 datos y
después de él también. La mediana se simboliza con las letras: Mdn.
Medidas de dispersión: Los estudios estadísticos permiten hacer inferencias de una característica de una población a partir de la información contenida en una muestra. Los métodos numéricos que describen a los conjuntos de observaciones tienen como objetivo dar una imagen mental de la distribución de frecuencias.
Una vez localizado el centro de la distribución de un conjunto de datos, lo que
procede es buscar una medida de dispersión de los datos.
La dispersión o variación es una característica importante de un conjunto de datos porque intenta dar una idea de cuál esparcidos se encuentran éstos.
Existen diversas medidas de dispersión, algunas de ellas son:
• Desviación estándar
• Varianza
a)Desviación estándar: La variación estándar es aquella que mide cuánto se separan los datos de la media aritmética, para datos no agrupados la fórmula es la siguiente:

Y en datos agrupados, Si x1, x2, …, xk ocurren con frecuencias f1, f2, …, fk, respectivamente, la desviación típica se expresa como:
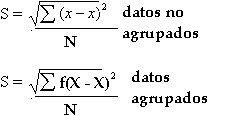
* La desviación estándar será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
* Si a todos los valores de la variable se les suma un número ladesviación estándar no varía.
* Si todos los valores de la variable se multiplican por un número ladesviación estándar queda multiplicada por dicho número.
* En los casos que no se pueda hallar la media tampoco será posible hallar la desviación estándar.
b)Varianza : Esta medida nos permite identificar la diferencia promedio que hay entre cada uno de los valores respecto a
su punto central (Media ).
La fórmula es practiczmente la misma que la de la desviación
estandar:

Es un valor estadístico que te permite ver que tan dispersos o
variaciones tienes entre las mediciones que estás realizando de un
grupo de datos.
Contesta:
¿Qué es la mediana ?
¿Cómo se simboliza la mediana ?
¿Cuántas y cuáles columnas deben agregarse a la tabla original para localizar la mediana en
¿Qué es la moda ?
¿Cómo se simboliza la moda?
BLOQUE X
Empleas los conceptos elementales de la probabilidad
Probabilidad clasica
Es el número de resultados favorables a la presentación de un evento dividido entre el número total de resultados posibles. La probabilidad clásica o teórica se aplica cuando cada evento simple del espacio muestral tiene la misma probabilidad de ocurrir. Si bien no podemos saber cuál va ser el resultado inal de un evento aleatorio, si podemos determinar cuáles son los resultados posibles para éste. Al conjunto de todos estos resultados posibles se les conoce como espacio muestral.
La fórmula para obtener la probabilidad clásica o teórica:

Probabilidad clásica de ocurrencia de uno u otro suceso
*Sucesos mutuamente excluyentes:
P(AoB) = P(A) + P(B)
![]()
*Sucesos no excluyentes:
P(AoB) = P(A) + P(B) - P(AÇ B)

Probabilidad condicional: En muchas ocaciones, la probabilidad de que ocurra un evento depende lo que ha ocurrido en otro evento. En este caso se tiene lo que se llama probabilidad condicional.
La probabilidad condicional de A, dado que ha ocurrido el evento B, se escribe P(A/B). Es decir, la probabilidad de que ocurra un evento A cuando se conoce cierta información relacionada con la ocurrencia de otro evento B.
P(A|B) probabilidad de que ocurra A dado que B ha ocurrido.
P(B|A) probabilidad de que ocurra B dado que A ha ocurrido.
Si P(B) >0, entonces la probabilidad condicional de A dado B es igual a:
 Ejemplo:
Ejemplo:
1. La siguiente tabla presenta el ascenso de los catedráticos de una institución durante los últimos 5 años.
Tabla de ascenso de catedráticos:
Hombres Mujeres Totales
Ascendido (A) 278 26 334
No ascendido (NA) 662 194 856
Totales 940 220 1160
a) Probabilidad de que un profesor escogido al azar sea ascendido dado que es hombre (H)
P(H)= 940/1160 = 0.81
P(HÇA) =278/1160 =.24
P(A/H) = P(AÇH) / P(H)= .24 / .81 =.30
b) Probabilidad de que un profesor escogido al azar sea ascendido dado que es mujer (M)
P(A/M)= 26/1160 =0.02
P(M)= 220/1160 = 0.19
P(A/M) = P(AÇM)/P(M)=.02/.19=.12
A partir de la fórmula de la probabilidad condicional, es posible derivar las fórmulas para la intersección de los eventos, a través del producto de dos probabilidades.
Para eventos dependientes:
P(AÇB) = P(B)* P(A/B) si P(B)=0
P(AÇB) = P(A)* P(B/A) si P(A)=0
Para eventos independientes
P(AÇB) = P(A) * P(B)
Simbología:
U = Unión
Ç = Intersección
| = Tal que
las áreas de los triángulos iguales.

- 20
- 5
- 4
- 3
cualquiera se divide en triángulos uniendo el centro
con cada uno de los vértices. La altura de cada uno
de los triángulos coincide con la apotema del
polígono. Se calcula el área de uno de estos
triángulos y se multiplica por el número de triángulos
que se han formado.
Perímetro de un polígono regular
Áreas de polígonos irregulares
Para calcular el área de un polígono irregular
cualquiera debemos basarnos en métodos indirectos.
Estos métodos, básicamente, son tres: el llamado
método de triangulación, el uso de una trama
cuadriculada o, en algunos casos, descomponer el
polígono en cuadriláteros conocidos.
Perímetro de un polígono irregular
- El diámetro divide a la circunferencia y al círculo en dos partes iguales.
- El diámetro es la mayor cuerda de la circunferencia.
- · En una circunferencia, o en circunferencias iguales, a cuerdas iguales corresponden arcos iguales, y si dos cuerdas son desiguales, a la mayor corresponde mayor arco.
- · La tangente a una circunferencia es perpendicular al radio en el punto de contacto.
- MEDIDA DE UN ÁNGULO INSCRITO. La medida de todo ángulo inscrito es igual a la mitad del arco comprendido entre sus lados.
- MEDIDA DE UN ÁNGULO SEMIINSCRITO: La medida del ángulo semiinscrito es igual a la mitad del arco comprendido entre sus lados.
- MEDIDA DEL ÁNGULO INTERIOR. la medida del ángulo interior es igual a la semisuma de las medidas de los arcos comprendidos por sus lados y por sus prolongaciones.
- MEDIDA DEL ÁNGULO EXTERIOR: La medida del ángulo exterior es igual a la semidiferencia de las medida de los arcos comprendidos por sus lados.
LOS ÁNGULOS EN LA CIRCUNFERENCIA
Podemos dibujar ángulos que se relacionen con la circunferencia. Según la posición que ocupen reciben nombres apropiados con relación a esa posición.
Cuanto se refiere a los ÁNGULOS en la circunferencia, siempre RELACIONAMOS a éstos con los ARCOS que forman.
1) Ángulo central: nos hemos referido a él en más de una ocasión; se trata del ángulo formado por dos radios que son sus lados y su vértice se encuentra en el centro O de la circunferencia.
En la figura siguiente ves que el arco  corresponde al ángulo central Ô que lo representamos con el acento circunflejo
corresponde al ángulo central Ô que lo representamos con el acento circunflejo  sobre la letra que representa el vértice del ángulo.
sobre la letra que representa el vértice del ángulo.

El arco  corresponde al ángulo central
corresponde al ángulo central  o lo que es lo mismo, la longitud del arco comprendido entre sus lados (los radios) pertenece al ángulo central
o lo que es lo mismo, la longitud del arco comprendido entre sus lados (los radios) pertenece al ángulo central  y su medida es de 96º.
y su medida es de 96º.
Cuanto mayor es el ángulo central mayor será la longitud del arco que abarcan sus lados:
Cuanto mayor es el ángulo central mayor será la longitud del arco que abarcan sus lados:

Vas a tener en cuenta que cuando representamos con letras un ángulo, por ejemplo  significa que la letra señalada con
significa que la letra señalada con  en este caso la O, nos referimos a que el vértice del ángulo se encuentra en dicha letra.
en este caso la O, nos referimos a que el vértice del ángulo se encuentra en dicha letra.
Cuando nos refiramos a un arco entre dos puntos señalados con letras, por ejemplo: el arco entre los puntos A y B lo representamos: 
Las dos circunferencias de la última figura de igual radio, la longitud del arco vemos que están en razón directa con la medida del ángulo central: a mayor medida del ángulo central corresponde mayor longitud de arco. La longitud  es decir, a 50º corresponde el arco
es decir, a 50º corresponde el arco  y a 111º corresponde
y a 111º corresponde  y puedes comprobar que a mayor ángulo central corresponde mayor longitud de arco.
y puedes comprobar que a mayor ángulo central corresponde mayor longitud de arco.
Muchas veces cuando nos referimos a las medidas de los arcosde la circunferencia hablamos de lo que miden sus longitudes en: m., dm., cm., pero también podemos referirnos a su medida en grados, minutos y segundos, incluso en radianes.
Cuando decimos que un arco mide 75º12’13’’ quiere decir que su ángulo entral tiene la misma medida.
Las medidas de los arcos de la última figura puedes expresarlos también en grados: el arco Muchas veces cuando nos referimos a las medidas de los arcosde la circunferencia hablamos de lo que miden sus longitudes en: m., dm., cm., pero también podemos referirnos a su medida en grados, minutos y segundos, incluso en radianes.
Cuando decimos que un arco mide 75º12’13’’ quiere decir que su ángulo entral tiene la misma medida.
Las medidas de los ángulos y arcos de una circunferencia se miden en grados, minutos y segundos.
15.144 Una circunferencia tiene un radio de 5 m. ¿Cuánto mide un arco de esta circunferencia que corresponde a un ángulo central 60º?
Respuesta: 5,23 m.
Solución:
La longitud total de la circunferencia  m., corresponde a 380º
m., corresponde a 380º
Una longitud de………………………..X m. corresponden a 60º
Una longitud de………………………..X m. corresponden a 60º

15.145 ¿Cuál es la longitud de un arco en metros sabiendo que su ángulo central vale 65º y su radio 8 m.?
Respuesta: 9,07 m.
2) Ángulo inscrito: es el ángulo que tiene su vértice en un punto de la misma línea de la circunferencia y sus lados la cortan.

Ves que el vértice se encuentra en el punto P de la circunferencia y los lados del ángulo inscrito cortan a la circunferencia en A y en B.
¿Cuál es la medida del arco correspondiente a este ángulo inscrito de 44º? Por supuesto que no se trata de la longitud del arco
Modo de calcular el valor de un ángulo inscrito:
En primer lugar trazo una línea que une el punto B con el centroO, tal como lo puedes ver en la figura siguiente:
En primer lugar trazo una línea que une el punto B con el centroO, tal como lo puedes ver en la figura siguiente:

El segmento OB y el segmento OP son iguales por tratarse del radio. Esto quiere decir que si los lados con vértice en O son iguales, los ángulos cuyos vértices están en B y en P serán iguales.
Las medidas de estos ángulos los tienes a continuación y comprobamos que tienen 44º:
Las medidas de estos ángulos los tienes a continuación y comprobamos que tienen 44º:

Ahora observa bien la figura siguiente que como estudiamos con anterioridad e hicimos la demostración correspondiente sobre elvalor de un ángulo exterior de un triángulo, decíamos que eraigual a la suma de los otros dos ángulos interiores no adyacentes:

El ángulo con vértice en O es igual a los valores de los ángulos cuyos vértices están en B y en P, podríamos escribir: 
Vemos que los ángulos  ambos valen en nuestro ejemplo 44º.
ambos valen en nuestro ejemplo 44º.
La igualdad  podemos escribirla
podemos escribirla  por ser iguales los ángulos
por ser iguales los ángulos 
Esto quiere decir que  podemos escribir:
podemos escribir:  y de esta igualdad despejamos
y de esta igualdad despejamos  :
:

Comprobamos que el ángulo central en  vale 88º, es decir, el doble que los ángulos inscritos
vale 88º, es decir, el doble que los ángulos inscritos  y abarca el arco
y abarca el arco  Esto significa que la medida del arco que abarca el ángulo
Esto significa que la medida del arco que abarca el ángulo  o el ángulo
o el ángulo  valdrán la mitad de lo que abarca el ángulo central
valdrán la mitad de lo que abarca el ángulo central  ,es decir,
,es decir,  .
.
El valor de un ángulo inscrito es igual a la mitad del ángulo central, luego, la medida del arco correspondiente a un ángulo inscrito equivale a la mitad del arco que comprenden sus lados o a la mitad del ángulo central correspondiente.
3) Ángulo semi-inscrito: El ángulo semi-inscrito es el que su vértice se encuentra en un punto de la circunferencia, y sus lados, uno es tangente y el otro secante con relación a la circunferencia:

En la figura siguiente señalamos el centro y creamos el ángulo central  . El lado
. El lado  del ángulo central es perpendicular allado secante
del ángulo central es perpendicular allado secante  . El lado
. El lado  del ángulo central es perpendicular al lado tangente
del ángulo central es perpendicular al lado tangente  :
:

Pasamos a la figura siguiente y puedes ver que hemos creado los ángulos  que abarca el arco
que abarca el arco  y
y  que abarca el arco
que abarca el arco  , es decir, los ángulos en
, es decir, los ángulos en  y en
y en  . Estos ángulos son iguales (en este caso miden 46º) porque sus lados son perpendiculares:
. Estos ángulos son iguales (en este caso miden 46º) porque sus lados son perpendiculares:

El arco  corresponde al ángulo central
corresponde al ángulo central  de 46º. Podemos escribir:
de 46º. Podemos escribir:
Como el valor del arco correspondiente al ángulo central es el que abarcan sus lados escribimos:
También podemos decir que:
Como el arco  es la mitad del arco
es la mitad del arco  podemos escribir:
podemos escribir:

Como  , podemos decir que también:
, podemos decir que también: Si ahora sustituyes :
Si ahora sustituyes :
 tenemos la igualdad :
tenemos la igualdad : 
La medida de un ángulo semi-inscrito es igual a la mitad del arco que abarcan los lados.
Todo lo explicado sobre el ángulo semi-inscrito lo puedes ver en el gráfico siguiente:
Todo lo explicado sobre el ángulo semi-inscrito lo puedes ver en el gráfico siguiente:

Perimetro y Area
Se llama Π= Pi al valor del cociente de la longitud de una circunferencia entre su diámetro. Su valor aproximado es 3,14. En realidad Π tiene infinitos decimales.
ejercicios
..
..
....
..
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Para las Funciones Trigonométricas, como se mencionó anteriormente,
haremos uso del Teorema de Pitágoras y trabajaremos con las Funciones
de Seno, Coseno y Tangente, y sus inversas, además de apoyarnos
siempre con la Calculadora.
Las letras minúsculas son las que utilizamos en el Teorema de Pitágoras,
las letras Mayúsculas, en éste caso, se utilizarán para referirnos a los
Ángulos del Triángulo.
Empezaremos a ver cada una de las Funciones:
1. Función Seno ( Sen):
La Función Seno nos describe la relación existente entre Lado Opuesto sobre la
Hipotenusa. Su simbología es la siguiente:
2. Función Coseno ( Cos):
La Función Coseno describe la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:
3. Función Tangente ( Tan):
Ésta Función nos representa la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:

También tenemos las Funciones que son inversas a las anteriores:
4. Función Cotangente ( Cot):
Que describe la relación entre Lado Adyacente con Lado Opuesto:
5. Función Secante ( Sec): Relación entre Hipotenusa sobre Lado Adyacente:
6. Función Cosecante ( CsC): Nos muestra la relación entre Hipotenusa sobre Lado Opuesto:
El sistema circular. En este sistema se usa como unidad el ángulo llamado
"radián". Un radián, es el ángulo cuyos lados comprenden un arco a la
circunferencia cuya longitud es igual al radio de la circunferencia. Un pi
radián equivale a 180° Para encontrar la medición de cualquier ángulo utilizamos
el transportador, que usualmente está dividido en 360 partes iguales y cada una
de esas partes equivalen a un grado, es decir, está en el sistema
sexagesimal.
Funciones
(razones) trigonométricas
|
|||
Directas
|
Recíprocas
|
||
sen
|
seno
|
cosec
(csc)
|
cosecante
|
cos
|
coseno
|
sec
|
secante
|
tan
(tg)
|
tangente
|
cotan
(cotg)
|
cotangente
|
En toda aplicación para la resolución de triángulos se proporcionan datos incompletos o se desconocen algunos de ellos, como en el caso de los ángulos o longitudes de catetos de un triángulo rectángulo. Al procedimiento de encontrar los valores restantes partiendo de los datos originales, se le conoce como "Resolución de un triángulo rectángulo" Para que esto se cumpla, debes resolver problemas sencillos donde apliques las razones trigonométricas para el uso de triángulos rectángulos y recordar el teorema de Pitágoras.
Resolver un triángulo es hallar sus lados, ángulos y área. Es necesario conocer dos lados del triángulo, o bien un lado y un ángulo distinto del recto.
1. Se conocen la hipotenusa y un cateto




Resolver el triángulo conociendo:
2. Se conocen los dos catetos



 Resolver el triángulo conociendo:
Resolver el triángulo conociendo:
3. Se conocen la hipotenusa y un ángulo agudo




Resolver el triángulo conociendo:
Ejercicios
1 Expresa en grados sexagesimales los siguientes ángulos:
1 3 rad
22π/5rad.
33π/10 rad.
2 Expresa en radianes los siguientes ángulos:
1316°
2 10°
3 127º
3 Sabiendo que cos α = ¼ , y que 270º <α <360°. Calcular las restantes razones trigonométricas del ángulo α.
4 Sabiendo que tg α = 2, y que 180º < α <270°. Calcular las restantes razones trigonométricas del ángulo α.
5 Sabiendo que sec α = 2, 0< α < /2, calcular las restantes razones trigonométricas.
/2, calcular las restantes razones trigonométricas.
6 Calcula las razones de los siguientes ángulos:
4 Sabiendo que tg α = 2, y que 180º < α <270°. Calcular las restantes razones trigonométricas del ángulo α.
5 Sabiendo que sec α = 2, 0< α <
6 Calcula las razones de los siguientes ángulos:
1225°
2 330°
3 2655°
4 −840º
7Comprobar las identidades:
1
2
3
4
5
8 De un triángulo rectángulo ABC, se conocen a = 5 m y B = 41.7°. Resolver el triángulo
9De un triángulo rectángulo ABC, se conocen b = 3 m y B = 54.6°. Resolver el triángulo.
10De un triángulo rectángulo ABC, se conocen a = 6 m y b = 4 m. Resolver el triángulo.
11De un triángulo rectángulo ABC, se conocen b = 3 m y c = 5 m. Resolver el triángulo.
12Un árbol de 50 m de alto proyecta una sombra de 60 m de larga. Encontrar el ángulo de elevación del sol en ese momento.
13Un dirigible que está volando a 800 m de altura, distingue un pueblo con un ángulo de depresión de 12°. ¿A qué distancia del pueblo se halla?
14Hallar el radio de una circunferencia sabiendo que una cuerda de 24.6 m tiene como arco correspondiente uno de 70°
15Calcular el área de una parcela triangular, sabiendo que dos de sus lados miden 80 m y 130 m, y forman entre ellos un ángulo de 70°.
16 Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa bajo un ángulo de 30° y si nos acercamos 10 m, bajo un ángulo de 60°.
17 La longitud del lado de un octógono regular es 12 m. Hallar los radios de la circunferencia inscrita y circunscrita.
9De un triángulo rectángulo ABC, se conocen b = 3 m y B = 54.6°. Resolver el triángulo.
10De un triángulo rectángulo ABC, se conocen a = 6 m y b = 4 m. Resolver el triángulo.
11De un triángulo rectángulo ABC, se conocen b = 3 m y c = 5 m. Resolver el triángulo.
12Un árbol de 50 m de alto proyecta una sombra de 60 m de larga. Encontrar el ángulo de elevación del sol en ese momento.
13Un dirigible que está volando a 800 m de altura, distingue un pueblo con un ángulo de depresión de 12°. ¿A qué distancia del pueblo se halla?
14Hallar el radio de una circunferencia sabiendo que una cuerda de 24.6 m tiene como arco correspondiente uno de 70°
15Calcular el área de una parcela triangular, sabiendo que dos de sus lados miden 80 m y 130 m, y forman entre ellos un ángulo de 70°.
16 Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa bajo un ángulo de 30° y si nos acercamos 10 m, bajo un ángulo de 60°.
17 La longitud del lado de un octógono regular es 12 m. Hallar los radios de la circunferencia inscrita y circunscrita.
BLOQUE VII
Aplicas las funciones trigonométricas
Funciones trigonométricas en el plano cartesiano: De acuerdo con el cuadrante en que se halle el lado terminal del ángulo y teniendo en cuenta que la distancia de un punto cualquiera al origen de coordenadas es siempre positiva, y aplicando la "ley de los signos", las funciones trigonométricas pueden ser positivas o negativas.
En la tabla de la parte inferior se resumen los signos de las funciones trigonométricas en cada uno de los cuadrantes.
Sen(x) positivo en cuadrantes I y II porque en ambos el cateto opuesto es positivo.
Sen(x) negativo en cuadrantes III y IV porque en ambos el cateto opuesto es negativo.
Cos(x) positivo en cuadrantes I y IV porque en ambos el cateto ayacente es positivo.
Cos(x) negativo en cuadrantes II y III porque en ambos el cateto adyacente es negativo.
Tan(x) positivo en cuadrantes I y III porque ambos catetos tienen igual signo
Tan(x) negativo en cuadrantes II y IV porque ambos catetos tienen distintos signos
seno
|
coseno
|
tangente
|
cotangente
|
secante
|
cosecante
| |
I
|
+
|
+
|
+
|
+
|
+
|
+
|
II
|
+
|
-
|
-
|
-
|
-
|
+
|
III
|
-
|
-
|
+
|
+
|
-
|
-
|
IV
|
-
|
+
|
-
|
-
|
+
|
-
|
Círculo unitario
Como el radio del círculo unitario es 1, entonces la circunferencia del círculo es:
Función seno
Dominio:
Recorrido: [−1, 1]
Período:
Continuidad: Continua en
Impar: sen(−x) = −sen x
Dominio:
Recorrido: [−1, 1]
Período:
Continuidad: Continua en 
Par: cos(−x) = cos x
Dominio:
Recorrido:
Continuidad: Continua en
Período:
Impar: tg(−x) = −tg x
Dominio:
Recorrido:
Continuidad: Continua en
Período:
Impar: cotg(−x) = −cotg x
Dominio:
Recorrido: (− ∞, −1][1, ∞)
Período:
Continuidad: Continua en
Par: sec(−x) = sec x
Dominio:
Recorrido: (− ∞, −1]  [1, ∞)
[1, ∞)
Período:
Continuidad: Continua en
Impar: cosec(−x) = −cosec x
Ejemplo 2: Dado dos ángulos y un lado incluído (ALA).
Dado A = 42°, B = 75° y c = 22 cm. Encuentre el ángulo y los lados faltantes.
Ejemplo 1: No existe solución
Dado a = 15, b = 25 y A = 80°. Encuentre los otros ángulos y el lado.
Ejemplo 2: Dos soluciones existen
Dado a = 6. b = 7 y A = 30°. Encuentre los otros ángulos y el lado.
Ejemplo 3: Una solución existe
Dado a = 22, b =12 y A = 40°. Encuentre los otros ángulos y el lado.| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 20) | 15 | 1 | 15 |
| [20, 30) | 25 | 8 | 200 |
| [30,40) | 35 | 10 | 350 |
| [40, 50) | 45 | 9 | 405 |
| [50, 60 | 55 | 8 | 440 |
| [60,70) | 65 | 4 | 260 |
| [70, 80) | 75 | 2 | 150 |
| 42 | 1 820 |


Probabilidad clásica de ocurrencia de uno u otro suceso
*Sucesos mutuamente excluyentes:
P(AoB) = P(A) + P(B)
*Sucesos no excluyentes:
P(AoB) = P(A) + P(B) - P(AÇ B)
Probabilidad condicional: En muchas ocaciones, la probabilidad de que ocurra un evento depende lo que ha ocurrido en otro evento. En este caso se tiene lo que se llama probabilidad condicional.
La probabilidad condicional de A, dado que ha ocurrido el evento B, se escribe P(A/B). Es decir, la probabilidad de que ocurra un evento A cuando se conoce cierta información relacionada con la ocurrencia de otro evento B.
P(A|B) probabilidad de que ocurra A dado que B ha ocurrido.
P(B|A) probabilidad de que ocurra B dado que A ha ocurrido.
Si P(B) >0, entonces la probabilidad condicional de A dado B es igual a:
Ejemplo:
1. La siguiente tabla presenta el ascenso de los catedráticos de una institución durante los últimos 5 años.
Tabla de ascenso de catedráticos:
Hombres Mujeres Totales
Ascendido (A) 278 26 334
No ascendido (NA) 662 194 856
Totales 940 220 1160
a) Probabilidad de que un profesor escogido al azar sea ascendido dado que es hombre (H)
P(H)= 940/1160 = 0.81
P(HÇA) =278/1160 =.24
b) Probabilidad de que un profesor escogido al azar sea ascendido dado que es mujer (M)
P(A/M)= 26/1160 =0.02
P(M)= 220/1160 = 0.19
P(A/M) = P(AÇM)/P(M)=.02/.19=.12
A partir de la fórmula de la probabilidad condicional, es posible derivar las fórmulas para la intersección de los eventos, a través del producto de dos probabilidades.
Para eventos dependientes:
P(AÇB) = P(B)* P(A/B) si P(B)=0
P(AÇB) = P(A)* P(B/A) si P(A)=0
Para eventos independientes
P(AÇB) = P(A) * P(B)
Simbología:
U = Unión
Ç = Intersección
| = Tal que









